Introduzione
Fig. 1 – Confronto fra PDF di una distribuzione di valori normale (in azzurro), e PDF dei suoi valori di massima e di minima (rispettivamente in arancione e giallo).
Teoria di base
Distribuzione di Gumbel
Distribuzione di Fréchet
Distribuzione di Weibull
Distribuzione di valori estremi generalizzata
- Per $k = 0$, la distribuzione generalizzata è assimilabile a una di tipo I, o Gumbel
- Per $k > 0$, la distribuzione generalizzata è assimilabile a una di tipo II, o Fréchet
- Per $k < 0$, la distribuzione generalizzata è assimilabile a una funzione di tipo III, o Weibull inversa. La funzione di tipo III, infatti, è appropriata per modellare valori massimi, mentre la comune distribuzione Weibull è applicata a valori minimi.
Fig. 2 – Come varia la forma della distribuzione di valori estremi generalizzata al variare del parametro k.
Dimostrazioni dei legami tra distribuzione generalizzata e distribuzioni di Gumbel, Fréchet e Weibull
Gumbel
Per $k=0$, allora la funzione PDF generalizzata si trasforma in
$$\begin{align}f(x) &= \frac{1}{\sigma}\exp\left(-\frac{x-\mu}{\sigma}\right)\exp\left(-\exp\left(-\frac{x-\mu}{\sigma}\right)\right)\\&=\frac{1}{\sigma}\exp\left(-\frac{x-\mu}{\sigma}-\exp\left(-\frac{x-\mu}{\sigma}\right)\right)\end{align}$$
Ovvero la PDF di Gumbel per valori massimi.
Fréchet
Per $k>0$, sia $\alpha = \frac{1}{k} > 0$ e $y = 1 + k\frac{x-\mu}{\sigma} \Rightarrow \frac{x-\mu}{\sigma} = \frac{1 – y}{k}$, allora la distribuzione generalizzata assume la forma
$$\begin{align}f(y)&=\frac{1}{\sigma}\left[1 + \frac{1}{\alpha}\left(\frac{y-1}{\frac{1}{\alpha}}\right)\right]^{-\alpha\left(1+\frac{1}{\alpha}\right)}\exp\left( -\left[1 + \frac{1}{\alpha} \left( \frac{y – 1}{\frac{1}{\alpha}}\right) \right] ^{-\alpha} \right)\\&=\frac{1}{\sigma}y^{-1-\alpha}\exp(-y^{-\alpha})\\&=\frac{1}{\sigma}\left(\frac{1}{y}\right)^{1+\alpha}\exp\left(-\left(\frac{1}{y}\right)^{\alpha}\right)\end{align}$$
Ovvero quella della distribuzione di Fréchet.
Weibull
Per $k<0$, sia $\alpha = -\frac{1}{k} > 0$ e $y = 1 – \lvert k \rvert\frac{x-\mu}{\sigma} \Rightarrow \frac{x-\mu}{\sigma} = \frac{1 – y}{\lvert k \rvert}$, allora la distribuzione generalizzata assume la forma
$$\begin{align}f(y)&=\frac{1}{\sigma}\left[1 – \frac{1}{\alpha}\left(\frac{1 – y}{\frac{1}{\alpha}}\right)\right]^{\alpha\left(1-\frac{1}{\alpha}\right)}\exp\left( -\left[1 – \frac{1}{\alpha} \left( \frac{1 – y}{\frac{1}{\alpha}}\right) \right] ^{\alpha} \right)\\&=\frac{1}{\sigma}y^{\alpha – 1}\exp(-y^{\alpha})\end{align}$$
Ovvero quella della distribuzione di Weibull inversa.
Esempio 1: calcolo della probabilità del livello massimo di un fiume

Fig. 3 – PDF del modello Fréchet applicato ai dati di innalzamento del livello del fiume.

Fig. 4 – Calcolo della probabilità di innalzamento del livello del fiume.
Esempio 2: modellazione della resistenza alla tensione di una trave
- il test Kolmogorov-Smirnov modificato (KSM),
- il test del P-value,
- e il test del Chi quadrato.
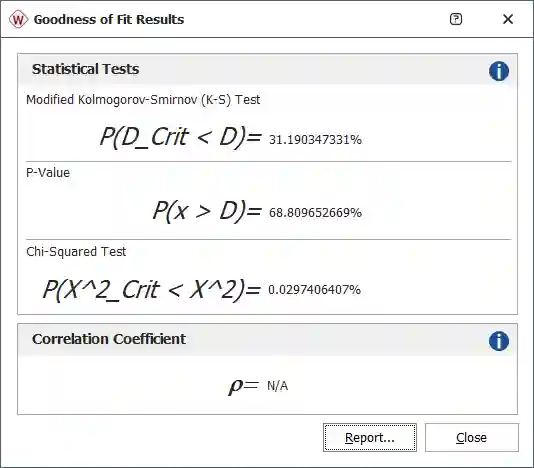
Sia il test KSM che il test del Chi quadrato ritornano la differenza di probabilità tra la probabilità osservata e la probabilità prevista. Più il risultato è vicino a 1, più significativa sarà la distanza tra i due risultati, e più problematico sarà giustificare la corrispondenza tra modello e dati reali. La figura 5 mostra un confronto fra i test “Goodness of fit” delle distribuzioni Gumbel e Weibull. Dall’analisi dei risultati dei due modelli si può osservare che, in questo caso, la distribuzione più appropriata da utilizzare sia la distribuzione Weibull. Questa scelta è corroborata anche dall’analisi empirica del fitting dei punti delle funzioni di densità cumulativa in figura 6; il fitting della funzione Weibull risulta molto più preciso rispetto a quello della funzione Gumbel.
Goodness of fit test per la distribuzione Gumbel.
Goodness of fit test per la distribuzione Weibull.
Fig. 5 – Confronto fra “Goodness of fit test” di una distribuzione Gumbel e una distribuzione Weibull.
Fig. 6 – Confronto fra distribuzioni cumulative: Gumbel e Weibull.
Conclusione
Riferimenti
https://web.archive.org/web/20150103123125/http://www.mathwave.com/articles/extreme-value-distributions.html