Articoli correlati
Analisi Fault Tree e applicazioni
Introduzione
In questo articolo discuteremo le applicazioni di fault tree. La Fault Tree Analysis è uno strumento estremamente utile che trova applicazioni in analisi di sicurezza e rischio attraverso un approccio top-down. Essa consiste nella creazione di un grafico ad albero, la cui radice rappresenta il top event, cioè un evento indesiderato che compromette l’affidabilità o la sicurezza del sistema. La metodologia Fault Tree si affianca al metodo di analisi RBD nel quantificare un problema e si può dire che ne sia la versione speculare. Un RBD modella una sequenza di successi e l’unità strutturale è il blocco. Esso rappresenta un componente indivisibile del sistema, e ne modella il funzionamento in combinazione con altri blocchi. La Fault Tree Analysis, invece, modella una sequenza di guasti e le unità principali che la compongono sono gli eventi che portano con la loro combinazione al top event, ovvero evento indesiderato. Tali eventi sono legati tra loro attraverso relazioni booleane rappresentate da porte logiche comunemente utilizzate in ingegneria elettronica.
Per una trattazione introduttiva all’analisi Fault Tree, si consiglia la lettura dell’articolo ‘Nuovo alla Fault Tree?‘.
Fault Tree analysis statiche, con funzioni statistiche e dinamiche
Esistono diverse modalità per rappresentare un sistema complesso attraverso un albero dei guasti. In questo articolo vedremo esempi delle tre principali, ovvero:
- Fault Tree statica
- Fault Tree con funzioni statistiche
- Fault Tree dinamica
I primi due esempi mostreranno un albero dei guasti analitico, la cui un’osservazione si ferma al primo guasto. L’ultimo, invece, si baserà su una simulazione del comportamento dei componenti e delle porte nel tempo. Per semplicità sono state omesse le riparazioni degli eventi.
Fault Tree statica
In una Fault Tree statica, tutti gli eventi occorrono secondo probabilità immutabili nel tempo. Sebbene questo approccio risulti molto semplice e immediato, esso non tiene conto dei fenomeni di usura o invecchiamento dei componenti durante il loro utilizzo. È dunque buona norma avvalersi del metodo statico solo in caso di analisi di eventi con una probabilità costante nel tempo.
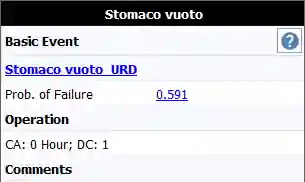
Figura 1. La probabilità che questo evento avvenga è un valore fisso di 0.591.
Consideriamo come esempio un top event “malattia”, Il quale può essere causato da un’infezione per via animale, oppure da disturbi all’apparato digestivo (porta OR 1). A propria volta, l’infezione può avvenire solamente dopo una puntura di zanzara, e se in quell’occasione non si indossava una maglietta a maniche lunghe (porte AND e NOT). Il malessere all’apparato digestivo, invece, può essere causato dall’ingestione di cibo avariato, oppure dal consumo di alcol a stomaco vuoto (Porte OR 2 e INH). La porta INH rappresenta un evento che avviene solamente se si verifica una condizione imprescindibile, ovvero essere a digiuno (evento “stomaco vuoto”).
Il risultato della Fault Tree è quello di osservare come la combinazione degli eventi descritti porti all’insorgere della malattia (top event). Tale metodologia è molto utile per il calcolo della probabilità di accadimento del top event in fase di studio.
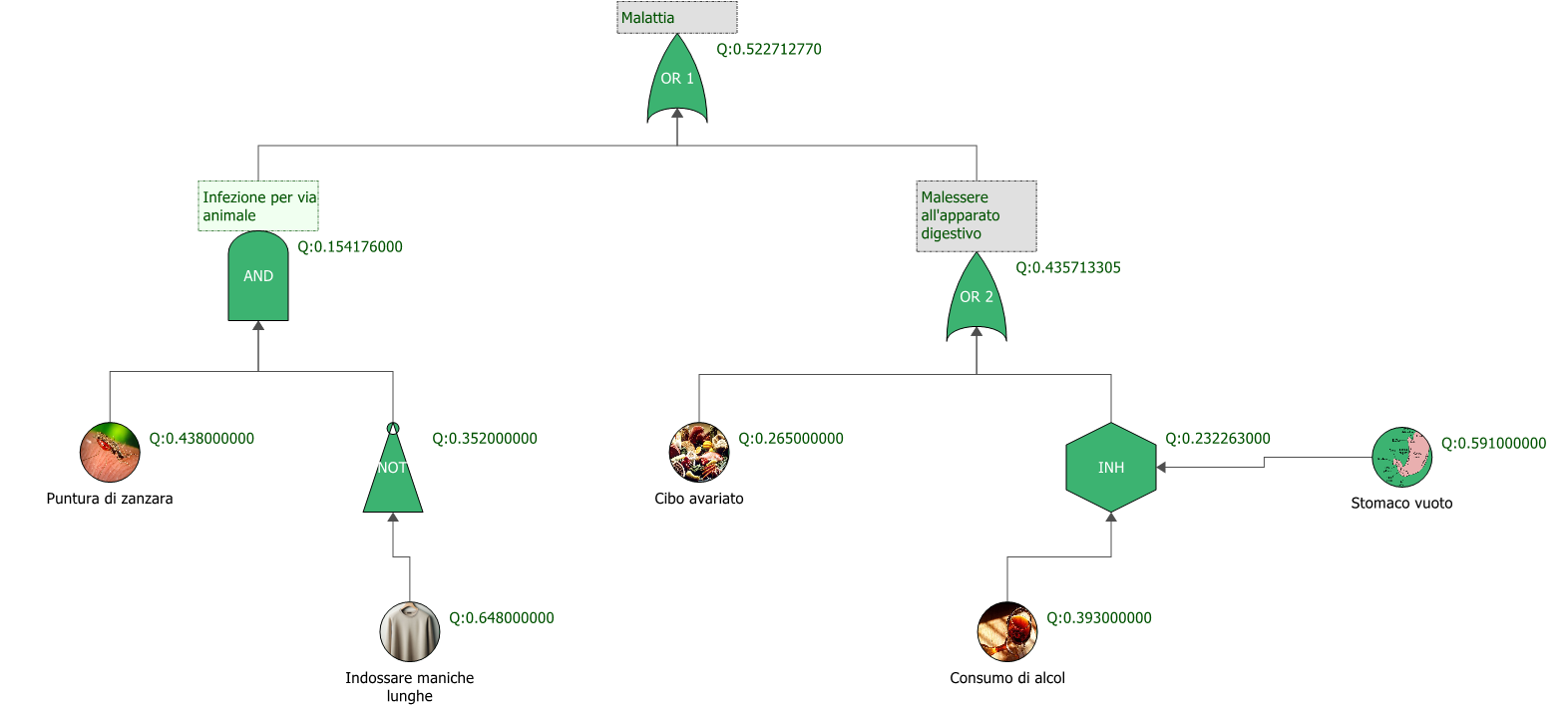
Figura 2. Fault Tree che mostra le possibili cause di una malattia.
La figura 2 mostra il valore Q, che all’interno dell’ecosistema ReliaSoft indica la probabilità di guasto.
Significato di “Q” nella Fault Tree
Compiendo una ricerca sul significato di Q nelle analisi Fault Tree, è possibile imbattersi in definizioni discordanti. Questo simbolo rappresenta comunemente l’indisponibilità del sistema nel tempo, Q(t), o indisponibilità media, Q. Come accennato in precedenza, tuttavia, i prodotti ReliaSoft associano a questo termine il significato di probabilità di guasto, per cui \(Q(t) = 1 – R(t)\), con R(t) definita come affidabilità del sistema.
Fault Tree analysis con funzioni statistiche
Un’evoluzione dell’approccio statico alle Fault Tree è rappresentata dall’uso delle funzioni di guasto comunemente utilizzate in ingegneria dell’affidabilità, come la Weibull o la lognormale. Esse permettono di modellare in maniera più realistica i componenti del sistema (e di conseguenza gli eventi) poiché tengono conto della variazione della probabilità di accadimento nel tempo. È estremamente importante ricordare di non inserire sia probabilità fisse che funzioni di guasto all’interno della stessa Fault Tree, poiché si rischia di confrontare dei fattori che mutano nel tempo con fattori costanti, arrivando poi a risultati poco sensati.
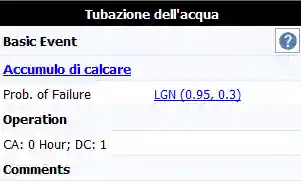
Figura 3. Evento a cui è assegnata una funzione di probabilità dipendente dal tempo, specificamente una funzione lognormale.
La figura 4 mostra una Fault Tree sviluppata a partire da un guasto di una caldaia a condensazione. Il top event è la mancata produzione di acqua calda. Essa risulta causata da una mancanza di acqua o gas a monte, un guasto alla parte elettronica che ne compromette il funzionamento, o un mancato scambio di calore (porta OR 1). La Fault Tree si sviluppa ulteriormente tramite porte OR e AND, fino alla definizione degli eventi di base che hanno causato il guasto a monte, come ad esempio l’accumulo di calcare nella pompa dell’acqua, o l’ostruzione del bruciatore.
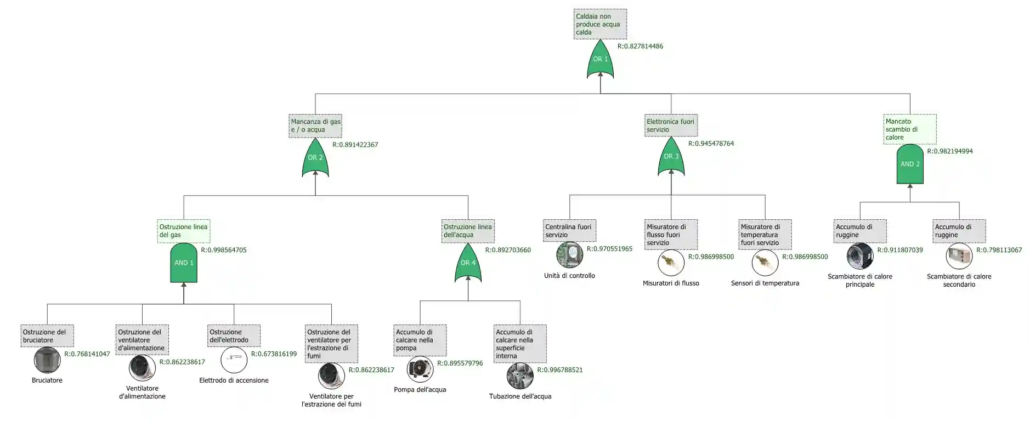
Fig 4. Fault Tree di una caldaia. Il top event è la “mancata produzione di acqua calda”
Nella figura seguente si può osservare come all’evento base sia associata una funzione di guasto dipendente dal tempo. La scelta delle funzioni statistiche più appropriate è un aspetto fondamentale che Tecram insegna nel corso RS250.
Fault Tree analysis dinamica
L’ultima tipologia di Fault Tree si definisce dinamica. In questo ambiente, gli eventi sono influenzati non solo dalle proprie funzioni di guasto, ma anche da altri eventi che avvengono durante il funzionamento del sistema. Queste interazioni sono modellate tramite porte logiche speciali. Esse, possono forzare una ben definita sequenza di funzionamento. Oppure, scatenare a loro volta eventi solo in determinate condizioni. Una breve dimostrazione di una di queste porte, la porta INH, è già avvenuta nel paragrafo precedente.
La figura sottostante mostra un modello di Fault Tree dinamica basata su un sistema antincendio, la quale impiega tre porte dinamiche:
- Sequence enforcing gate: definisce una sequenza con cui devono verificarsi gli eventi sottostanti, avvenuti i quali si manifesta l’evento in output. A questa porta è necessario collegare almeno un elemento attivo e uno in standby, il quale si attiverà solo dopo il guasto dell’elemento attivo.
- Standby gate: similmente alla porta SEQ, a questa sono collegati uno o più eventi, sia attivi che in standby, che si verificano in un ordine preciso. Il suo funzionamento è analogo a un contenitore standby in RBD, il quale è utile per modellare componenti ridondanti allo scopo di migliorare l’affidabilità del sistema.
- Load sharing gate: definisce una spartizione del carico di lavoro tra diversi eventi di base, oltre che al numero di componenti funzionanti affinché la porta risulti attiva (votazione k-su-n). Se si dovessero verificare eventi che determinano guasti a un numero di componenti maggiore di quello specificato, la porta si disattiverebbe. Questa porta funziona analogamente al ‘load sharing container’ in RBD, il quale raggruppa componenti che possono dividersi un carico di lavoro fino a una situazione di sovraccarico che causa un guasto definitivo.
- Priority AND gate: non utilizzata nel diagramma rappresenta una porta AND particolare in quanto solo una determinata sequenza di rotture porta alla attivazione della porta Priority AND gate.
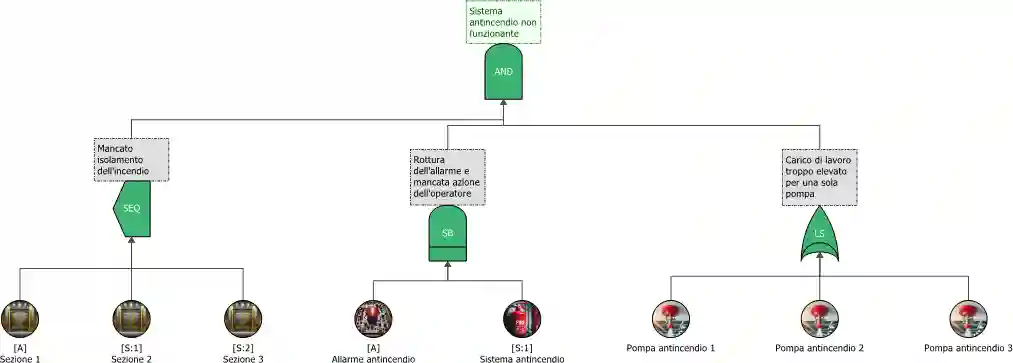
Figura 5. Diagramma Fault Tree di un sistema antincendio.
Nell’esempio sopra, figura 5, la porta SEQ modella il mancato isolamento di un incendio in sezioni concentriche di un reparto di produzione. Le fiamme iniziano a propagarsi dalla sezione 1, per poi invadere le sezioni successive. La porta standby, invece, rappresenta un malfunzionamento del sistema antincendio. L’allarme è attivo fino al suo guasto, e l’operatore non si accorge dell’accensione del sistema di notifica antincendio di riserva. Infine, la porta load sharing modella i guasti delle pompe antincendio. In condizioni normali i tre componenti condividono il carico. In base al criterio di progettazione si imposta il sovraccarico massimo sopportabile dalla singola pompa. In questo esempio, almeno due pompe sono necessarie a far fronte al carico. Il guasto alla seconda pompa porta il sistema ad disattivarsi.
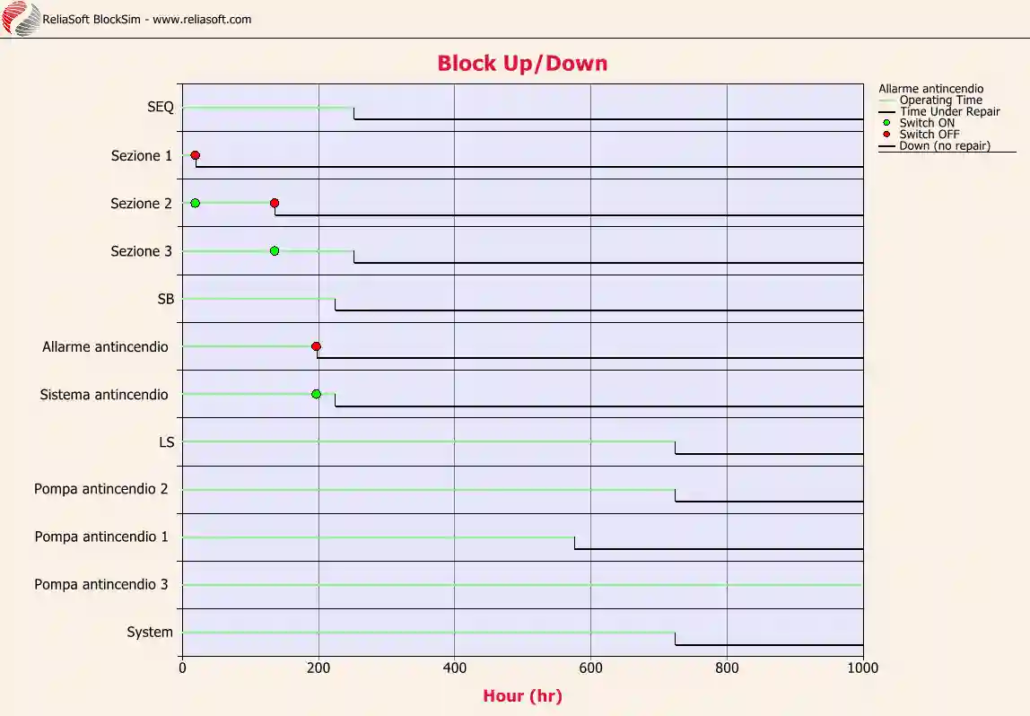
Figura 6. Diagramma temporale relativo al malfunzionamento del sistema antincendio.
Nella figura 6 possiamo osservare l’evoluzione nel tempo del comportamento del sistema mano a mano che i suoi componenti si guastano. I cerchi rossi indicano il guasto di un blocco attivo, con il conseguente passaggio del testimone a un blocco in standby, contrassegnato da cerchi verdi. Una linea verde chiaro indica un componente funzionante, mentre una linea nera ne indica uno fuori uso.
Differenza tra analisi FMEA e Fault Tree
Sia l’analisi FMEA che la Fault Tree Analysis sono strumenti fondamentali per lo sviluppo delle analisi di rischio. Esistono, tuttavia, delle differenze sostanziali tra i due processi:
- l’analisi FMEA analizza ciascun componente del sistema ‘dal basso’, e delinea le cause e le conseguenze dei guasti. È un approccio qualitativo, per cui è responsabilità dell’ingegnere assegnare un risk priority number adeguato a ciascuna modalità di guasto. Soffre di soggettività, ma per questo motivo non può essere sottostimata. Un’analisi FMEA determina come verrà sviluppato un prodotto e più viene svolta con rigore e con la giusta partecipazione, minori saranno le insorgenze di un richiamo prodotto sul mercato.
- La Fault Tree Analysis analizza un unico guasto, il top event, e ne determina le cause scatenanti e la loro probabilità di occorrenza. Vengono tuttavia escluse le conseguenze, le quali debbono essere analizzate tramite un albero degli eventi speculare all’albero dei guasti (disponibile come add-on del programma BlockSim). È un metodo quantitativo probabilistico, il che lo rende sistematico e più facilmente ripetibile. La Fault Tree analysis nella maggior parte dei casi è un’attività che si sviluppa a seguito dell’analisi FMEA come processo di Risk Assesment o di valutazione quantitativa del rischio.
Sebbene i risultati numerici di una Fault Tree Analysis appaiano appetibili per la creazione di reportistica efficace e convincente, questi possono risultare fuorvianti nel caso in cui non siano aggiornati, o le ipotesi su cui si basano non si verifichino. Uno studio FMEA compiuta da personale esperto, invece, può offrire una visione basata su ragionamenti ponderati, e un giudizio più dettagliato di un semplice valore numerico.
Tecram offre il workshop WKS08 a tutti coloro che abbiano un particolare interesse ad approfondire la propria conoscenza sulle analisi di rischio.
Conclusione
La Fault Tree è un valido strumento utilizzato per quantificare numericamente la probabilità di accadimento di un evento indesiderato (termine Q) che normalmente si associa ad un guasto. Questo articolo esamina le tre principali tipologie di Fault Tree attraverso semplici esempi: statica, con funzioni statistiche e dinamica. Le Fault Tree statiche sono un approccio che appartiene al passato e sono poco utilizzate in quanto gli eventi sono ritenuti statici e non variabili nel tempo. Sia l’uso di fault tree classiche (OR, AND, Votazione) mediante funzioni statistiche che le più avanzate fault tree dinamiche, sono molto comuni in quanto possono meglio rappresentare le cause che portano al Top Event.
Sebbene la Fault Tree sia un metodo quantitativo, l’analisi FMEA, con impostazione qualitativa, è ugualmente valida. Tuttavia, questa validità regge se e solo se, il personale partecipante alla sessione, ha le dovute competenze tecniche. L’analisi FMEA, a differenza della Fault Tree sviluppa la cosidetta “cause-consequence” analysis identificando sia le cause dell’insorgenza di un guasto che le sue conseguenze.
Appendice: la differenza fra probabilità di guasto e indisponibilità
Probability of Failure o probabilità di guasto indicata come Q(t) Quantile oppure F(t) Failure
Grandezza attribuibile ad un sistema non riparabile che mostra la probabilità che il sistema stesso NON sia in grado di adempiere la sua funzione (qualunque essa sia stata definita nella FMEA). Matematicamente rappresenta il complemento della funzione di survival o di affidabilità il cui simbolo è universalmente accettato come R(t)
Unavailability (indisponibilità) – anch’esso un valore di probabilità ma complicato dal fatto che a differenza della probabilità di guasto, che è unica, deriva dall’Availability (disponibilità) come suo complemento che però esiste in 6 varianti. Nello specifico,
- Disponibiità istantanea – A(T=t)
- Disponibilità media – A(t)
- Disponiblità intrinseca – A(I)
- Disponibilità stazionaria – A(∞) (condizione stazionaria)
- Disponibilità ottenuta – A(A) (condizione stazionaria)
- Disponibilità operativa – A(O) (condizione stazionaria)
Da notare che 3 definizioni non hanno alcun valore a meno che il sistema non abbia raggiunto una condizione stazionaria.
Consideriamo un solo caso: la disponibilità media che non richiede una condizione stazionaria del sistema (vedasi corso RSW300 per un’esplorazione dettagliata di queste tematiche)
Mean Unavailability = 1 – Mean Availability o meglio 1- A(t). Non esiste un’unità di misura universalmente riconosciuta per il termine Unavailability
Il termine disponibilità media rappresenta la porzione di tempo durante una missione (0, T] in cui il sistema/prodotto/componente è disponibile (cioè funzionante).
Il suo complemento (mean unavailbility) rappresenta la porzione di tempo durante una missione (0, T] in cui il sistema/prodotto/componente NON risulta disponibile. Questo può dipendere da diverse ragioni che non sono necessariamente dovute a rottura. Sulla base degli eventi che vengono inclusi come causa dell’indisponibilità, fioriscono appunto diverse definizioni di disponibilità.
In sommario, sia probabilità di guasto Q(t) o F(t) che l’indisponiblità 1-A(t) rappresentano valori di probabilità viste da angolazioni diverse:
- la prima riguarderà una finestra di tempo limitata in quanto il sistema/prodotto/componente sarà soggetto a guasti e questa andrà quindi aumentando con il tempo.
- La seconda, dipenderà in parte dal numero di simulazioni per raggiungere un valore medio stazionario e potrà includere qualsiasi tempo t poiché terrà conto di attività legate alla manutenzione del sistema considerato.